347
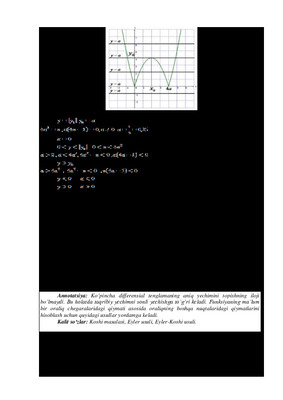
Tenglama ildizlari uchun quyidagi gipotezalar boʻladi:
1)
da 3 ta (ikkita musbat , bitta manfiy) ildizga ega boʻladi.
2)
da yagona ildizga ega boʻladi.
3)
,
da 4 ta (3 ta musbat, 1ta manfiy) ildizga ega boʻladi.
4)
da 2 ta (biri musbat ikkinchisi manfiy) ildizga ega boʻladi.
5)
da
da yechimga ega bo‘lmaydi.
6)
da
da kamida ikkita ildizga ega boʻladi.
Foydalanilgan adabiyotlar roʻyxati:
1. A.U.Abduhamidov, H.A.Nasimov , U.M.Nosirov, J.H.Husanov Algebra va matematik analiz
asoslari I,II-qism Akademik litseylar uchun darslik.1995 yil.
2. I.Isroilov, Z,Pashayev Geometrya I,II-qism Akademik litseylar uchun darslik.
ОDDIY DIFFERENSIAL TENGLAMALARNI SONLI YECHISH
Nuraliyev Toʻlqin Alimardanovich
Oʻzbekiston Milliy universitetining Jizzax filiali
―Amaliy matematika‖ kafedrasi oʻqituvchisi
Xandamov Yigitali Xolmirza oʻgʻli
Oʻzbekiston Milliy universitetining Jizzax filiali
―Amaliy matematika‖ kafedrasi oʻqituvchisi
Annotatsiya:
Koʻpincha differensial tenglamaning aniq yechimini topishning iloji
bo‘lmaydi. Bu holatda taqribiy yechimni sonli yechishga to‘g‘ri keladi. Funksiyaning ma‘lum
bir oraliq chegaralaridagi qiymati asosida oraliqning boshqa nuqtalaridagi qiymatlarini
hisoblash uchun quyidagi usullar yordamga keladi.
Kalit soʻzlar:
Koshi masalasi, Eyler usuli, Eyler-Koshi usuli.
Oddiy differensial tenglamalar uchun boshlang‘ich shartlarning berilishiga ko‘ra ikki xil
boladi. Funksiyaning biron bir oraliqning chegarasidagi yoki bitta nuqtadagi qiymati berilgan
bo‘ladi. Oraliqning chegarasida qiymatlari berilgan bo‘lsa, chegaraviy masala, bitta nuqtada
qiymatlari berilgan bo‘lsa, Koshi masalasi deyiladi.
Biz oddiy differensial tenglama uchun qo‘yilgan Koshi masalasini Eyler usulida yechishni
ko‘rib chiqamiz[1].

348
1-misol.
y´=x
2
+2y;
y(0)=1
Koshi masalasining [0;0,4] oraliqda
h
=0,1 qadam bilan yechimini topamiz.
Yechish. Differensial tenglamaning o‘ng tomoni:
f(x,y)=x
2
+2y;
Boshlang‘ich qiymatlar:
x
0
=0; y
0
=1;
Yechim aniqlanishi lozim bo‘lgan [
a;b
]oraliq:
a=0; b=0,4;
Oraliqning bo‘linish soni:
n=4; h=0,1.
x
i+1
= x
i
+h;
∆y
i
=h
*
f(x
i
;y
i
); y
i+1
=y
i
+∆y
i
;
(i=0;1;2;3)
Ushbu rekurrent formulalar bilan quyidagilarni topamiz:
1-qadam:
i=0; x
1
= x
0
+h=0+0,1=0,1; ∆y
0
=h
*
f(x
0
;y
0
)=0,1
*
(x
2
0
+2
*
y
0
)=
=0,1
*
(0
2
+2
*
1)=0,2; y
1
=y
0
+∆y
0
=1+0,2=1,2;
2-qadam:
i=1; x
2
= x
1
+h=0,1+0,1=0,2;
∆y
1
=h
*
f(x
1
;y
1
)=0,1
*
(x
2
1
+2
*
y
1
)=
=0,1
*
(0,1
2
+2
*
1,2)=0,241; y
2
=y
1
+∆y
1
=1,2+0,241=1,441;
3-qadam:
i=2; x
3
= x
2
+h=0,2+0,1=0,3;
∆y
2
=h
*
f(x
2
;y
2
)=0,1
*
(x
2
2
+2
*
y
2
)=
=0,1
*
(0,2
2
+2
*
1,441)=0,292; y
3
=y
2
+∆y
2
=1,441+0,292=1,733;
4-qadam:
i=3; x
4
= x
3
+h=0,3+0,1=0,4;
∆y
3
=h
*
f(x
3
;y
3
)=0,1
*
(x
2
3
+2
*
y
3
)=
=0,1
*
(0,3
2
+2
*
1,733)=0,3556; y
4
=y
3
+∆y
3
=1,733+0,3556=2,0886;
Shu oddiy differensial tenglama uchun qo‘yilgan Koshi masalasini Eyler-Koshi usulida
yechamiz[3].
2-misol.
y´=x
2
+2y;
y(0)=1
Koshi masalasining [0;0,4] oraliqda
h
=0,1 qadam bilan yechimini topamiz.
Yechish. Differensial tenglamaning o‘ng tomoni:
f(x,y)=x
2
+2y;
Boshlang‘ich qiymatlar:
x
0
=0; y
0
=1;
Yechim aniqlanishi lozim bo‘lgan [
a;b
]oraliq:
a=0; b=0,4;
Oraliqning bo‘linish soni:
n=4; h=0,1.
x
i+1
= x
i
+h;
y
i+1
=y
i
+∆y
i
;
(i=0;1;2;3)
∆y
i
=(K
i
(1)
+ K
i
(2)
)/2; K
i
(1)
=h
*
f(x
i
;y
i
); K
i
(2)
=h
*
f(x
i
+h;y
i
+K
i
(1)
);
Bu formulalar bilan quyidagilarni topamiz:
1-qadam:
i=0; x
1
= x
0
+h=0+0,1=0,1; K
0
(1)
=h
*
f(x
0
;y
0
)=0,1(0
2
+2
*
1)=0,2;
K
0
(2)
=h
*
f(x
0
+h;y
0
+K
0
(1)
)=0,1[(0+0,1)
2
+2
*
(1+0,2)]=0,1[0,01+2,4]=0,241;
∆y
0
=(K
0
(1)
+ K
0
(2)
)/2=(0,2+0,241)/2=0,441/2=0,2205;
y
1
=y
0
+∆y
0
=1+0,2205=1,2205;
2-qadam:
i=1; x
2
= x
1
+h=0,1+0,1=0,2;
K
1
(1)
=h
*
f(x
1
;y
1
)=0,1(0,1
2
+2
*
1,2205)=0,1(0,01+2,441)=0,245;
K
1
(2)
=h
*
f(x
1
+h;y
1
+K
1
(1)
)=0,1[(0,1+0,1)
2
+2
*
(1,2205+0,245)]=
0,1
*
[0,04+2,931]=0,1
*
2,971=0,2971;
∆y
1
=(K
1
(1)
+ K
1
(2)
)/2=(0,245+0,2971)/2=0,5421/2=0,27105;
y
2
=y
1
+∆y
1
=1,2205+0,27105=1,49155;
3-qadam:
i=2; x
3
= x
2
+h=0,2+0,1=0,3;
K
2
(1)
=h
*
f(x
2
;y
2
)=0,1(0,2
2
+2
*
1,49)=0,1(0,04+2,98)=0,302;
K
2
(2)
=h
*
f(x
2
+h;y
2
+K
2
(1)
)=0,1[(0,2+0,1)
2
+2
*
(1,49+0,302)]=
0,1
*
[0,09+3,584]=0,1
*
3,674=0,3674;
∆y
2
=(K
2
(1)
+ K
2
(2)
)/2=(0,302+0,3674)/2=0,6694/2=0,3347;
y
3
=y
2
+∆y
2
=1,49155+0,3347=1,85895;
4-qadam:
i=3; x
4
= x
3
+h=0,3+0,1=0,4;
K
3
(1)
=h
*
f(x
3
;y
3
)=0,1(0,3
2
+2
*
1,859)=0,1(0,09+3,718)=0,38;
K
3
(2)
=h
*
f(x
3
+h;y
3
+K
3
(1)
)=0,1[(0,3+0,1)
2
+2
*
(1,859+0,38)]=
0,1
*
[0,16+4,478]=0,1
*
4,638=0,4638;
∆y
3
=(K
3
(1)
+ K
3
(2)
)/2=(0,38+0,4638)/2=0,8438/2=0,4219;

349
y
4
=y
3
+∆y
3
=1,85895+0,4219=2,28085;
Hisoblangan ma‘lumotlarni jadvalda keltiramiz:
i
x
i
y
i
–
Eyler usulida
y
i
–
Eyler-Koshi usulida
Farqi
1
0,1
1,2
1,2205
0,0205
2
0,2
1,441
1,49155
0,05055
3
0,3
1,733
1,85895
0,12595
4
0,4
2,0886
2,28085
0,19225
Jadvaldan ko‘rinadiki, berilgan oraliqdagi
x
i
qiymatlariga mos Eyler va Eyler-Koshi
usullarida topilgan
y
i
taqribiy yechimlarning farqi 0,2 dan ortmaydi[2].
Foydalanilgan adabiyotlar roʻyxati:
1.
Isroilov
M.I.
Hisoblash
metodlari.
Toshkent,
Oʻqituvchi,
1-qism,
2003,
2-qism, 2008.
2.
Aloyev R.D., Xudoyberganov M.Oʻ. Hisoblash usullari kursidan laboratoriya
mashg‘ulotlari toʻplami. OʻzMU . Oʻquv qoʻllanma . 2008 y. 110 b.
3.
Xandamov,
Y.
(2020).
Система
моделирования
разрешения
и
совершенствования непрерывного образования. Архив Научных Публикаций JSPI.
NOANIQLIK SHAROITIDAGI BOSHQARUV TIZIMI UCHUN SILLIQMAS
TERMINAL FUNKSIONALNING XOSSALARI
1
Otakulov Salim,
2
Murotboyev Mirjalol Baxtiyor o‗g‗li
1
Fizika-matematika fanlari doktori, professor, Jizzax politexnika instituti
2
O‗zbekiston Milliy universitetining Jizzax filiali magistranti
Annotatsiya:
Ishda chiziqli dinamik tizimni tashqi ta‘sir parametrlari noaniqligi
sharoitida optimal boshqarish masalasi modeli qaralgan. Shu modelda maximin tipdagi
silliqmas terminal funksionalning ba‘zi xossalari o‗rganilgan.
Kalit so‗zlar:
boshqaruv tizimi modeli, noaniqlik sharoiti, terminal funksional, silliqmas
masala, optimal boshqaruv.
Boshqaruvning amaliy masalalari modellashtirilganda o‗lchash xatolari, tashqi kuchlar
ta‘siri, axborotning kechikishi va noaniqligi kabi bir qator muhim omillarni hisobga olish zarur
bo‗ladi. Amaliyot uchun muhim ahamiyatga ega bunday modellar tadqiqi noaniqlik sharoitidagi
optimal boshqarish masalalari matematik nazariyasining rivojlanishiga olib keldi [1,2,3].
Noaniqlik sharoitidagi tizimlarni boshqarish masalalarida asosiy yondashuvlardan biri –
sifat mezonining kafolatlangan qiymatiga erishish maqsadining qo‗yilishidan iborat. Bu esa
minimaksli meson bo‗yicha optimal boshqarishga, ya‘ni boshqarish sifatini miqdoriy baholovchi
maqsad funsionalining maksimumini minimallash masalasiga olib keladi [4,5]. Ushbu tipdagi
masalalarga xos muhim belgi – maqsad funsionalining silliqmasligidir. Bunday modellarga oid
tadqiqotlar natijasida silliqmas optimal boshqaruv masalalarini yeshish usullari rivojlanmoqda
[1-7].
2. Minimaksli masalaning qo‗yilishi.
R
n
– n
-o‗lchamli
)
,...,
(
1
n
x
x
x
vektorlar Yevklid
fazosi,
n
i
i
i
y
x
y
x
1
)
,
(
– bu fazoda vektorlar skalyar ko‗paytmasi,
2
1
)
(
1
2
n
i
i
x
x
–
n
R
x
vektorning normasi bo‗lsin. Holat vektori
n
R
х
bo‗lgan ob‘ektining harakati
]
,
[
,
)
(
)
(
)
(
1
0
t
t
t
v
t
C
u
t
B
x
t
A
x
(1)